Chapter 2 乱数

Exercise 2.1 R言語の組み込み関数runifを用いて，長さ\(1000\)の疑似一様乱数\(x_1, x_2,\ldots, x_{1000}\)を生成せよ．また，それらを\(1\times 1\)の二次元正方形に配置せよ，すなわち， \(xy\)平面上に，\(\{(x_1, x_2), (x_3, x_4), \ldots, (x_{999}, x_{1000})\}\)を描画せよ．

u <- matrix(runif(1000),nrow=2)
data.fr <- data.frame(x=u[1,], y=u[2,])
ggplot(data.fr,aes(x=x,y=y))+geom_point()+theme_bw()

なお，三次元への配置は次のようにしてできる．

set.seed(1234)
data.fr <- data.frame(x = runif(1e3), y = runif(1e3), z = runif(1e3))
plot_ly(data.fr, x=~x, y=~y, z=~z) %>% add_markers(marker=list(size=3))

さらに，RAND法の配置は次のようにすれば良い．三次元に配置すると問題が起きることも見える．

u <- numeric(3*1e3)
y <- 1234
n <- 2 ^ 31 - 1
a <- 65539
b <- 0

for(i in 1:length(u)){
  y <- (a * y + b) %% n
  u[i] <- y/n
}

u_mat <- matrix(u, nrow=3)
data.fr <- data.frame(x=u_mat[1,], y= u_mat[2,], z= u_mat[3,])
plot_ly(data.fr, x=~x, y=~y, z=~z) %>% add_markers(marker=list(size=3))

Exercise 2.2 \(a=13, b=0, n=67\)とし，初期値\(y_0=1234\)として線形合同法を用いて，長さ\(1000\)の疑似一様乱数\(x_1, x_2,\ldots, x_{1000}\)を生成せよ．また，上の問題と同じように，それらを\(1\times 1\)の二次元正方形に配置せよ，また，描画された点のうち，異なる点の数を数え上げよ．

u <- numeric(1e3)
y <- 1234
n <- 67
a <- 13
b <- 0
for(i in 1:length(u)){
  y <- (a * y + b) %% n
  u[i] <- y/n
}

u_mat <- matrix(u, nrow=2)
data.fr <- data.frame(x=u_mat[1,], y=u_mat[2,])
ggplot(data.fr,aes(x=x,y=y))+geom_point()+theme_bw()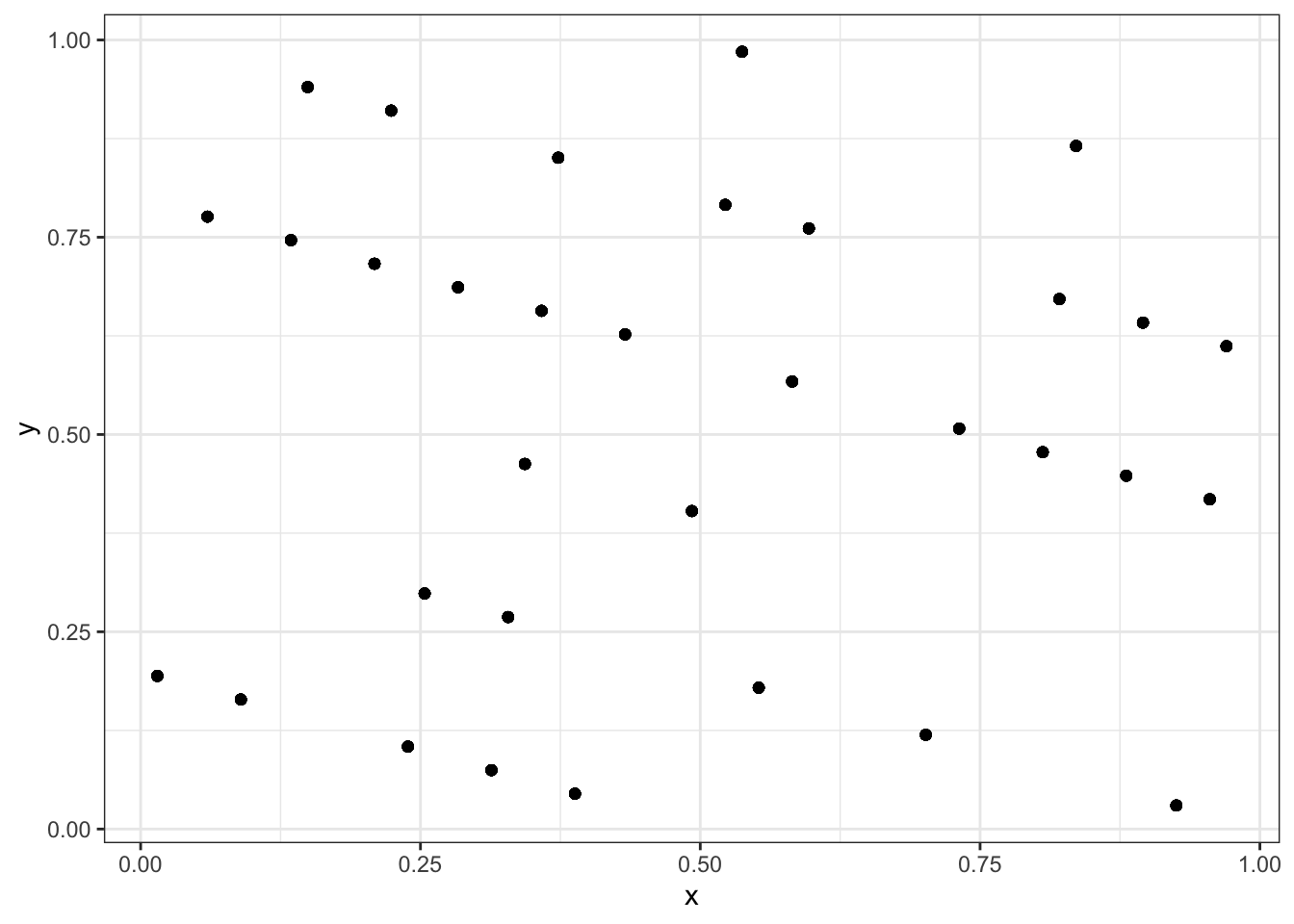

dim(unique(data.fr))[1] #No. of unique points

## [1] 33

Exercise 2.3 ロジスティック分布 (Logistic distribution)は \[\begin{equation}\nonumber%\label{eq:logistic_function} F(x)=\frac{e^x}{1+e^x}\ (-\infty<x<\infty) \end{equation}\] なる累積分布関数を持つ．R言語の組み込み関数runifを使ってロジスティック乱数を生成せよ．また，R言語の組み込み関数rlogisと計算時間の比較をおこなえ．

Solution. 逆変換法を使おう．累積分布関数の逆関数は \[ F^{-1}(u)=\log \frac{u}{1-u} \] だから，\(U\sim\mathcal{U}[0,1]\)なら\(F^{-1}(U)\)がロジスティック分布に従う．

f <- function(u){ return(log( u / (1 - u) ) )}
N <- 1e5
microbenchmark(A <- f(runif(N)), times = 100)

## Unit: milliseconds
##              expr      min       lq     mean   median       uq      max neval
##  A <- f(runif(N)) 2.030293 2.038626 2.275785 2.080542 2.401063 4.866459   100

microbenchmark(B <- rlogis(N), times = 100)

## Unit: milliseconds
##            expr      min       lq    mean   median       uq      max neval
##  B <- rlogis(N) 2.501584 2.511959 2.61694 2.541605 2.608646 5.695917   100

組み込み関数が\(10\%\)ほど速いようだ．

Exercise 2.4 \(a, b\)を正の実数とする．パレート分布 (Pareto distribution) の確率密度関数が \[ p(x;a,b)=\frac{ab^a}{x^{a+1}}\ (x\ge b) \] で与えられるとき，R言語の組み込み関数runifを用いてパレート乱数を生成する方法を記述せよ．

Solution. まず累積分布関数を計算しよう．定義どおり積分すると，任意の\(x\ge b\)に対し \[\begin{align*} F(x)&=\int_b^xp(y;a,b)\mathrm{d}y\\ &=\int_b^x\frac{ab^a}{y^{a+1}}\mathrm{d}y\\ &=b^a\left[-y^{-a}\right]_b^x =1-(x/b)^{-a}. \end{align*}\] したがって，累積分布関数の逆関数は \[ F^{-1}(u)=b/(1-u)^{1/a} \] となり，\(F^{-1}(U)=b/(1-U)^{1/a}\)で生成できる．ただし，\(U\)と\(1-U\)の従う確率分布は同じだから，\(b/U^{1/a}\)で生成できる．

a <- 2.0
b <- 1.0
N <- 1e5
f <- function(x) a*b^a/(x^(a+1))
data.fr <- data.frame(x = b/runif(N)^(1/a))
ggplot(data.fr, aes(x=x))+geom_histogram(aes(y=..density..), binwidth = 0.1, alpha=0.3)+theme_bw()+xlim(1,4)+stat_function(fun=f)

## Warning: Removed 6160 rows containing non-finite values (stat_bin).

## Warning: Removed 2 rows containing missing values (geom_bar).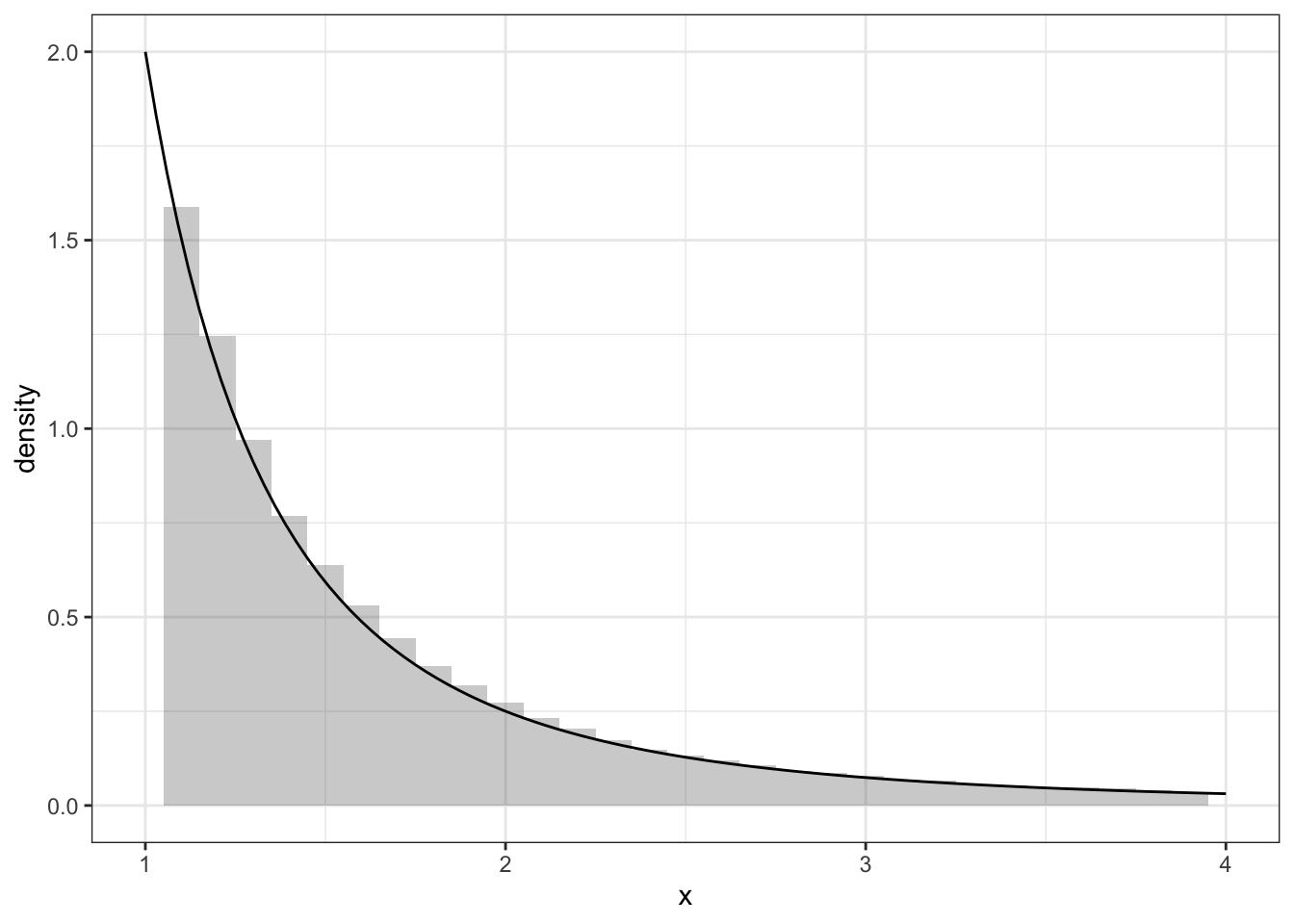

Exercise 2.5 \(\sigma\)は正の実数とする．レイリー分布 (Rayleigh distribution) の確率密度関数は \[ p(x;\sigma)=\frac{x}{\sigma^2}\exp(-x^2/2\sigma^2)\ (x\ge 0) \] で与えられる．R言語の組み込み関数runifを用いてレイリー乱数を生成する方法を記述せよ．

sigma <- 2.0
N <- 1e5
f <- function(x) x/sigma^2 * exp(-x^2/(2*sigma^2))
data.fr <- data.frame(x = sigma*sqrt(-2*log(runif(N))))
ggplot(data.fr, aes(x=x))+geom_histogram(aes(y=..density..),alpha=0.3,binwidth=0.1)+theme_bw()+stat_function(fun=f)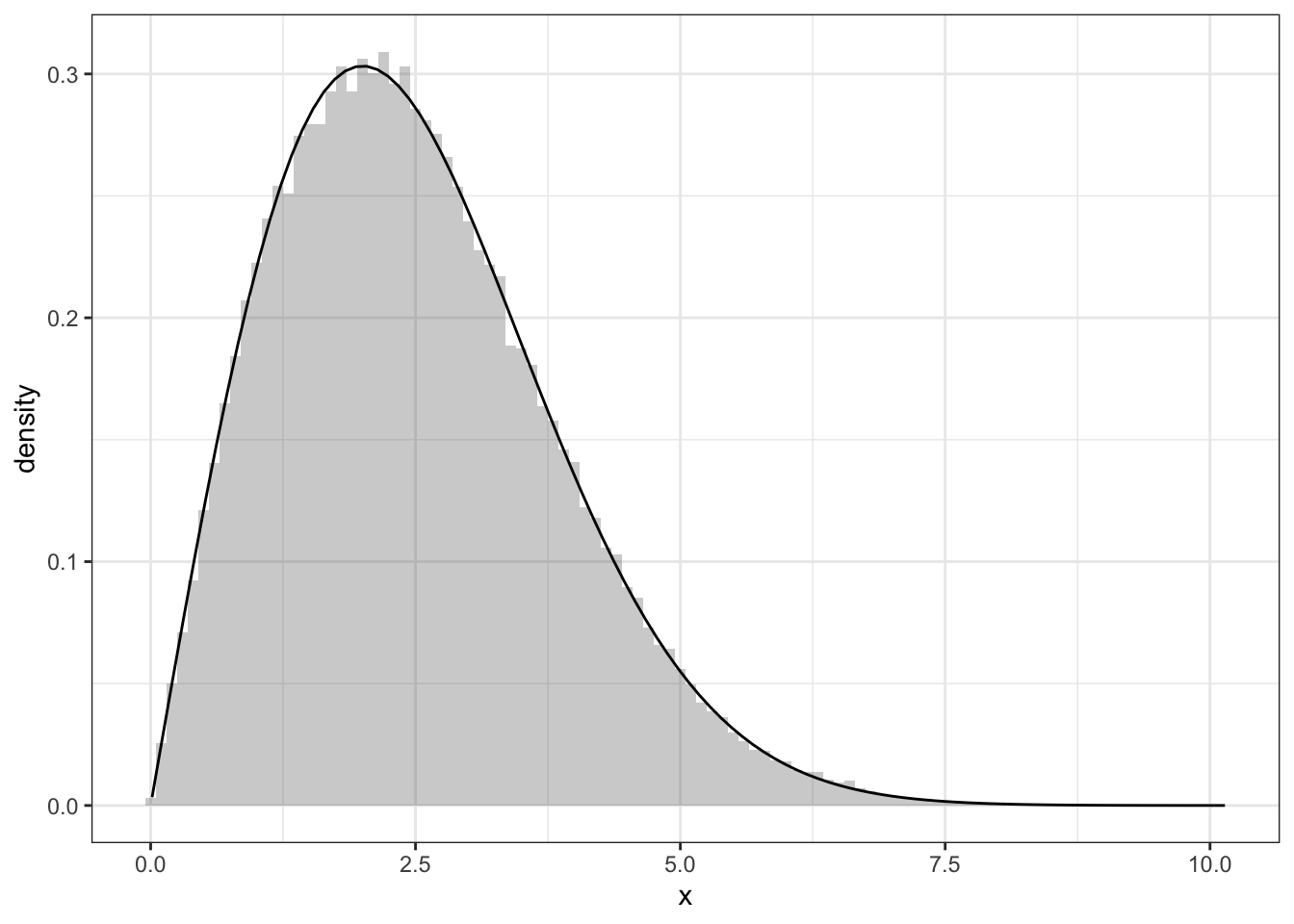

Exercise 2.6 \(a, b\)は正の実数とする．ワイブル分布 (Weibull distribution) の確率密度関数が \[ p(x;a,b)=\frac{a}{b^a}x^{a-1}e^{-(x/b)^a}\ (x\ge 0) \] で与えられる．R言語の組み込み関数runifを用いてワイブル乱数を生成する方法を記述せよ．

a <- 1.5
b <- 2.0
N <- 1e5
f <- function(x) a/b^a*x^(a-1)*exp(-(x/b)^a)
data.fr <- data.frame(x = b*(-log(runif(N)))^(1/a))
ggplot(data.fr, aes(x=x))+geom_histogram(aes(y=..density..),alpha=0.3,binwidth=0.1)+theme_bw()+stat_function(fun=f)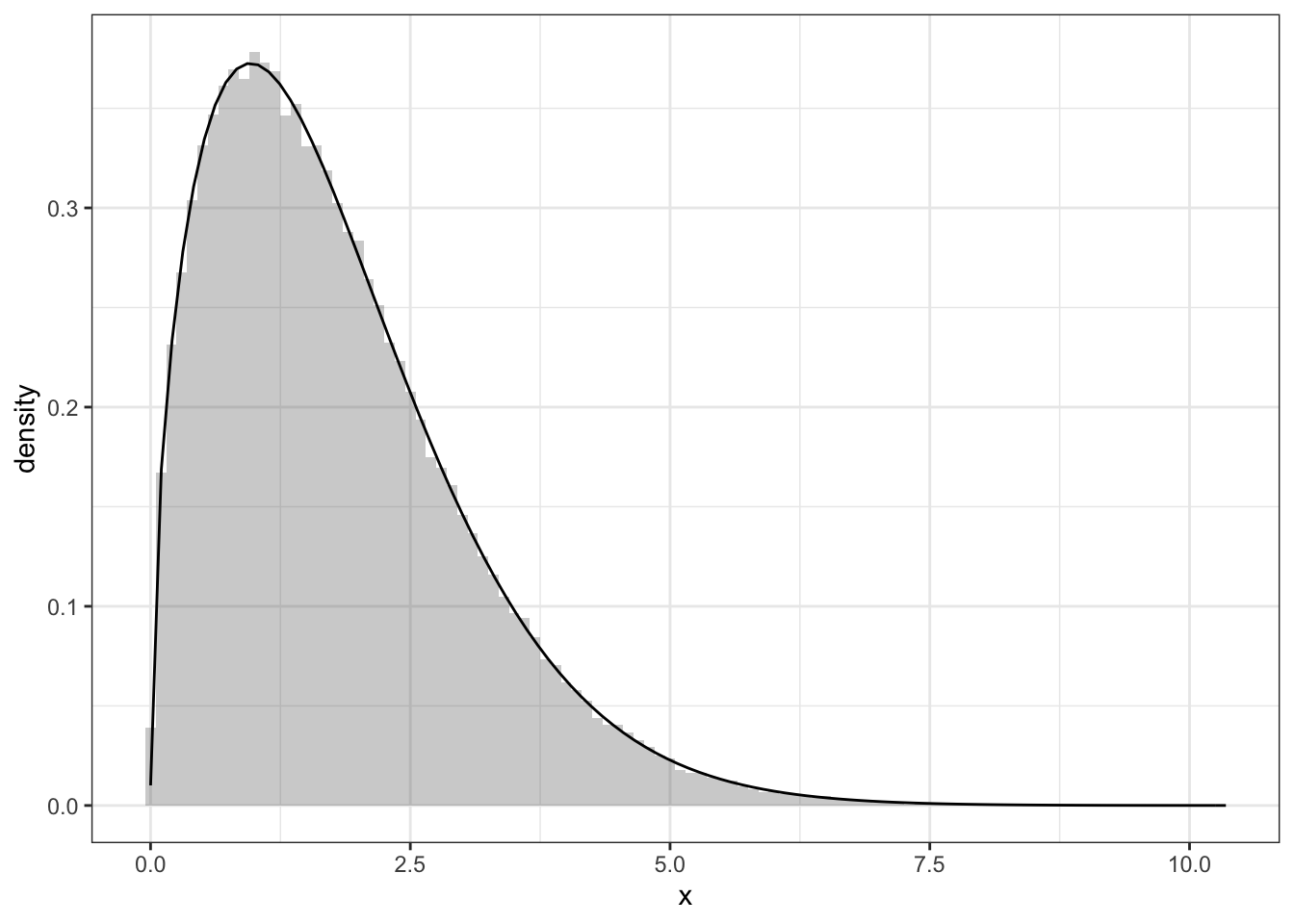

Exercise 2.7 \(N\)は正の整数，\(\theta\)は実数で\(0<\theta<1\)とする．二項分布\(\mathcal{B}(N,\theta)\)の確率関数は \[ p(n; N,\theta)=\binom{N}{n}\theta^n(1-\theta)^{N-n}\ (n=0,\ldots, N) \] で与えられる．R言語の組み込み関数runifを用いて二項分布 に従う乱数を生成する方法を記述せよ．

N <- 10
theta <- 0.6
F_seq <- cumsum(dbinom(0:N,N,theta))
f <- Vectorize(function(x) sum(x > F_seq))

data.fr <- data.frame(x=f(runif(1e4)))
ggplot(data.fr, aes(x))+geom_bar(aes(y=..prop..), alpha=0.5)+theme_bw()+stat_function(geom="point", fun=dbinom, args=list(size=N, prob=theta), n=11)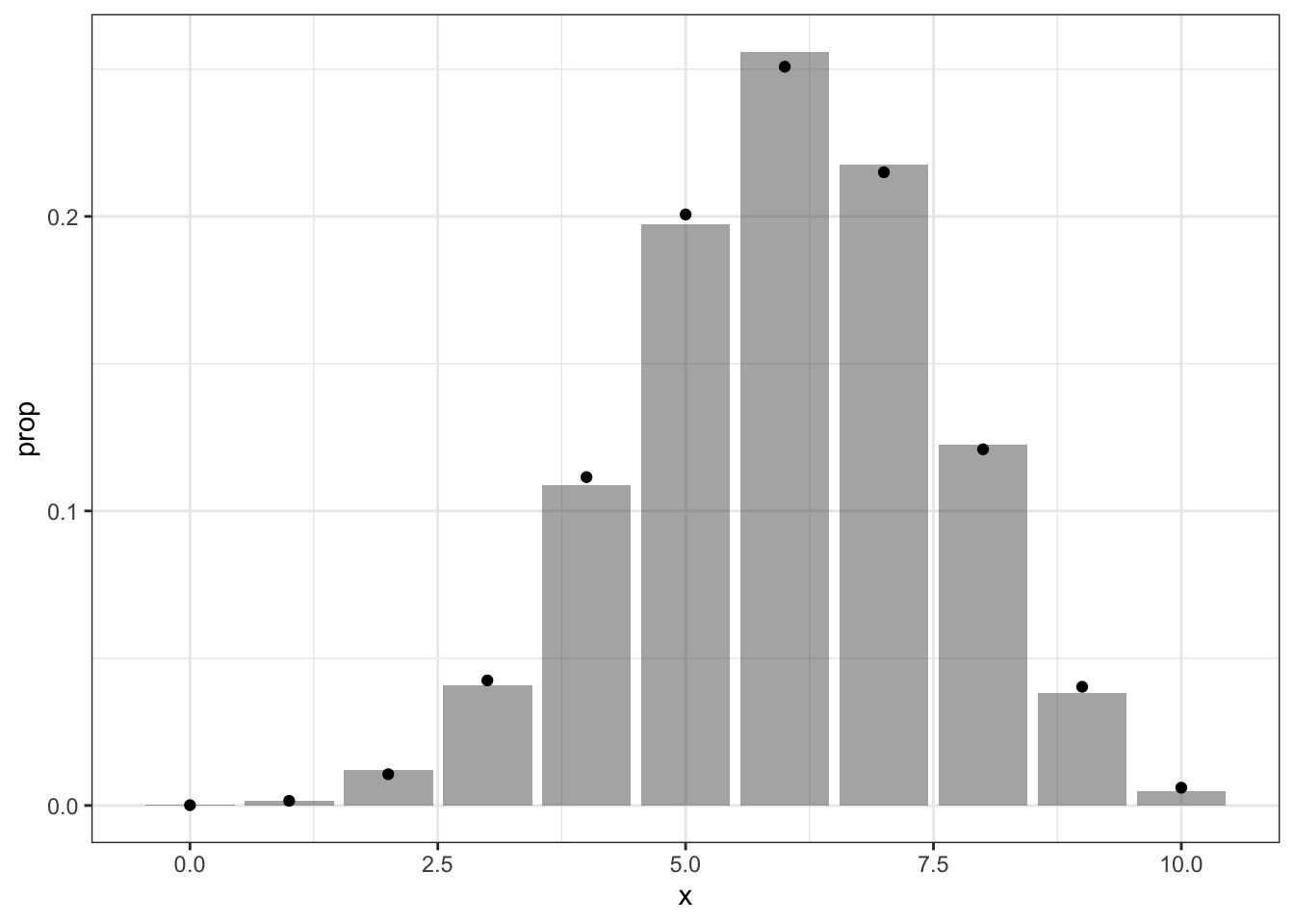

Exercise 2.8 \(r\)は正の整数，\(\theta\)は\(0<\theta<1\)を満たす実数とする．は確率関数 \[\begin{equation}\label{eq:neg_binom} p(n;r,\theta)=\binom{n+r-1}{n}(1-\theta)^r\theta^n\ (n=0,1,2,\ldots) \end{equation}\] を持つ．次の手続きで負の二項乱数が生成できることを示せ．必要があれば例1.9を参考にせよ．

r <- 10
y <- rgamma(1, shape = r, rate = (1-theta)/theta)
x <- rpois(1, y)

Solution. 上のRコードによれば，\(Y=y\)の条件のもと，確率変数\(X\)の従う分布は ポアソン分布\(\mathcal{P}(y)\)であり，確率関数は \[ p(x\mid y)=\frac{y^x}{x!}\exp(-y) \] である．さらに\(y\)は\(\mathcal{G}(r, (1-\theta)/\theta)\)に従う． \(X\)の周辺分布の確率密度関数は \[\begin{align*} \int_0^\infty p(x\mid y)p(y)\mathrm{d}y &= \int_0^\infty \frac{y^x}{x!}\exp(-y)\frac{1}{\Gamma(r)}\left(\frac{1-\theta}{\theta}\right)^ry^{r-1}\exp\left(-\frac{1-\theta}{\theta}y\right)\mathrm{d}y\\ &= \frac{1}{x!\Gamma(r)}\left(\frac{1-\theta}{\theta}\right)^r~\int_0^\infty y^{x+r-1}\exp\left(-\frac{1}{\theta}y\right)\mathrm{d}y\\ &= \frac{\Gamma(x+r)}{x!\Gamma(r)}\left(\frac{1-\theta}{\theta}\right)^r~\theta^{x+r} \end{align*}\] となる．ただし，教科書の式(1.7)を使った． あとは\(\Gamma(r)=(r-1)!, \Gamma(x+r)=(x+r-1)!\)であることから，式を見比べて結論が得られる．

Exercise 2.9 \(\alpha\)は正の実数とする．歪正規分布 (Skew normal distribution) は確率密度関数 \[ p(x)=2\phi(x)\Phi(\alpha x)\ (-\infty<x<\infty) \] を持つ．ただし\(\phi(x)，\Phi(x)\)は標準正規分布の確率密度関数および累積分布関数である．次の手続きで歪正規乱数が生成できることを示せ．

rho <- alpha ^ 2 / ( 1 + alpha ^2 )
w <- rnorm(2)
y <- sqrt( rho ) * w[1] + sqrt(1 - rho) * w[2]
x <- (y >= 0) * w[1] - (y < 0) * w[1] 

Solution. まず上の手続きを確率変数で書き直そう． \(W_1, W_2\)が独立で標準正規分布に従うとき， \[\begin{align*} Y&=\sqrt{\rho}~W_1+\sqrt{1-\rho}~W_2\\ X&= \left\{ \begin{split} W_1&\quad Y\ge 0\\ -W_1&\quad Y<0 \end{split} \right. \end{align*}\] 定める．ただし\(\rho=\alpha^2/(1+\alpha^2)\)である． 上の問題と同じように\(X\)の従う確率分布の周辺密度関数\(p(x)\)を計算したいが， \(Y, W_1\)を与えたもとでの\(X\)の分布が確定的なので同じようにはいかない．だから\(X\)の周辺分布の累積分布関数\(F(x)\)を求めて，それを微分することで周辺密度関数を導出しよう．

定義から \[ F(x)=\mathbb{P}(X\le x)=\mathbb{P}(W_1\le x, Y\ge 0)+ \mathbb{P}(-W_1\le x, Y< 0) \] である．じつは，右辺の２つの確率は同じだ．なぜなら\(W_1\)と\(W_2\)の符号を取り替えれば，ひとつめの事象とふたつめの事象が同じになるからだ．ここでは等号が入っているかどうかは小さいことなので気にしなくていい．だから． \[ F(x)=2\mathbb{P}(W_1\le x, Y\ge 0) \] となる． いっぽう，\(W_1=z\)をあたえたもとで， \[\begin{align*} \mathbb{P}(Y\ge 0\mid W_1=z)&=\mathbb{P}(\sqrt{\rho}~z+\sqrt{1-\rho}W_2\ge 0)\\ &=\mathbb{P}\left(W_2\ge -\sqrt{\frac{\rho}{1-\rho}}z\right)\\ &=\mathbb{P}\left(W_2\ge -\alpha~z\right)\\ &=1-\Phi(-\alpha z)=\Phi(\alpha z) \end{align*}\] となる．ここで，\(\Phi(x)\)は標準正規分布の累積分布関数で， \(1-\Phi(-x)=\Phi(x)\)を満たす．あとは\(W_1=z\)を\(z\le x\)の範囲で積分すれば \[ F(x)=2\int_{-\infty}^x\Phi(\alpha z)\phi(z)\mathrm{d}x \] となる．両辺を\(x\)で微分すれば， \[ p(x)=2\Phi(\alpha x)\phi(x). \]
ただしここで \[ \left(\int_{-\infty}^xf(z)\mathrm{d}z\right)'=f(x) \] という事実を使った．

Exercise 2.10 \(\lambda\)は正の実数とする．ラプラス分布 (Laplace distribution) は確率密度関数 \[ p(x;\lambda)=\frac{\lambda}{2}\exp(-\lambda |x|)\ (-\infty<x<\infty) \] を持つ確率分布である．両側指数分布を棄却法の提案分布として標準正規乱数を生成することを考える．このとき\(\lambda\)の関数として，式(2.6)の\(R\)を求め，\(R\)を最小にする\(\lambda\)を求めよ．

なお，式(2.6)とは \[\begin{align*} R=\sup_{x\in E}\frac{p(x)}{q(x)} \end{align*}\] のことであり，本問の場合は\(p(x)\)が標準正規分布の確率密度関数 \(\phi(x)=\exp(-x^2/2)/\sqrt{2\pi}\)で，\(q(x)\)が\(p(x;\lambda)\)である．

Solution. 上の\(R\)を\(\lambda\)の関数として， \[\begin{align*} R(\lambda)&=\sup_{x\in\mathbb{R}}\frac{\phi(x)}{p(x;\lambda)} \end{align*}\] とする．定義から \[\begin{align*} R(\lambda)&=\sup_{x\in\mathbb{R}}\frac{\exp(-x^2/2)/\sqrt{2\pi}}{\lambda 2^{-1}\exp(-\lambda|x|)}\\ &= \sqrt{2/\pi}\sup_{x\ge 0}\lambda^{-1}\exp(-x^2/2+\lambda x) \end{align*}\] となる．ただし，最後の等号では，\(\sup\)の中身が\(x=0\)について対称であることを使った．指数関数の中身を平方完成すると \[\begin{align*} R(\lambda)&= \sqrt{2/\pi}\sup_{x\ge 0}\lambda^{-1}\exp(\lambda^2/2)~\exp(-(x-\lambda)^2/2)\\ &=\sqrt{2/\pi}~\lambda^{-1}\exp(\lambda^2/2) \end{align*}\] である．あとは \[ f(\lambda)=\log\left(\sqrt{2/\pi}~\lambda^{-1}\exp(\lambda^2/2)\right) =\log\left(\sqrt{2/\pi}\right)-\log\lambda+\lambda^2/2 \] となる．\(f'(\lambda)=-1/\lambda+\lambda\)であり， \(\lambda=1\)で\(f\)は最小になることがわかる．よって\(R(\lambda)\)を最小にする\(\lambda\)は\(\lambda=1\).

maxr <- sqrt(2/pi)*1*exp(1/2) # R(lambda) = sup r(lambda)
r <- function(x) dnorm(x)/(dexp(abs(x))/2) # r(lambda)

n <- 1e4
vec <- numeric(1e2)

for(i in 1:n){
  
  x <- rexp(1) * (2*rbinom(1,1,0.5)-1) # Initial trial
  
  while(runif(1) > r(x)/maxr ){ # Rejection sampling
    x <- rexp(1) * (2*rbinom(1,1,0.5)-1)
  }
  vec[i] <- x
}

# Plot histgram vs density
t <- seq(-4,4,length=100)
fit <- dnorm(t)
fig <- plot_ly(x = vec, type="histogram", histnorm = "probability density", name="rejection method")
fig %>% add_lines(x = t, y = fit, mode = 'lines', name="pdf")

Exercise 2.11 (20211127追加）観測\(x\)は\(x\mid \theta\sim\mathcal{N}(\theta, 1)\)によって生成され，パラメータ\(\theta\)には事前分布\(\mathcal{C}(0,1)\)が定められている． \(\mathcal{C}(0, 1)\)を提案分布として，事後分布に従う乱数を棄却法を用いて生成せよ．

Solution. 教科書p64の通りに進めれば良い．事後分布は \[ p(\theta\mid x)= \frac{p(x\mid\theta)p(\theta)}{p(x)} \] となる．提案分布として事前分布を使うと，事後分布と提案分布の確率密度関数の割合\(r(\theta)\)は \[ r(\theta)=\frac{p(x\mid\theta)}{p(x)} \] となる．\(r(\theta)\)は\(\theta=\widehat{\theta}=x\)のとき最大になり，\(p(x\mid\theta)=\exp(-(x-\theta)^2/2)/\sqrt{2\pi}\)より，そのときの値は \[ R=\frac{p(x\mid\widehat{\theta})}{p(x)}=\frac{1}{\sqrt{2\pi}~p(x)} \] となる．したがって， \[ \frac{r(\theta)}{R}=\frac{p(x\mid\theta)}{p(x\mid\widehat{\theta})}=\exp\left(-\frac{(x-\theta)^2}{2}\right) \] となる．よって棄却法は次の手続きで実行できる．

• \(\theta\sim\mathcal{C}(0,1), U\sim\mathcal{U}[0,1]\)とする．

• \(U\le \exp\left(-\frac{(x-\theta)^2}{2}\right)\)のとき\(\theta\)を出力する．