Chapter 7 エラータム
7.1 エラータム第一刷
残念ながら本書(第一刷)でいくつかの誤りが見つかっている. 修正点の指摘について松野舜介氏に感謝します.
7.1.1 p44 例2.1について (20210308)
- 図2.4のキャプション:「パラメータ\(p=2\)の…」とあるのは「パラメータ\(\lambda=2\)の指数乱数のヒストグラム.黒い実線は指数分布の確率密度関数」の誤り.
7.1.2 p48 例2.3について (20200511)
実数の繰り上げ,繰り下げに関する議論に誤りがあった. \(\lceil x\rceil\)で\(x\)未満ではない最小の整数を表すとする.このとき\(1-(1-p)^x<U\)を満たす最大の整数は, \[ 1-U<(1-p)^x\leadsto\log(1-U)< x\log(1-p)\leadsto \frac{\log(1-U)}{\log(1-p)}>x \] より, \[ x=\left\lceil\frac{\log(1-U)}{\log(1-p)}-1\right\rceil \] とすべきだ.だから,乱数は \[ \left\lceil\frac{\log U}{\log(1-p)}-1\right\rceil \] で生成できる.R言語では
## [1] 1 0 1とすべきだった.ただし,教科書にある \[ \left [\frac{\log U}{\log(1-p)}\right] \] と先程の値が異なる確率は\(0\)だから,乱数生成の意味では問題を生じ得ない.
7.1.4 p93 練習問題3.2について (20210308)
\(\int_a^b(x-a)^2\mathrm{d}x=\int_a^b(x-b)^2\mathrm{d}x=(b-a)^3/3\)とすべき.
7.1.6 p109 例4.6について (20210308)
恥ずかしながら一部計算ミスしていた.以下に差し替える.
実数\(\alpha,\beta\)および正の実数\(\sigma\)を定める.\(\alpha^2+\beta^2\sigma^2\neq \alpha\)とする.初期値\(X_0=x_0\)にたいし,\(m=0,1,\ldots\)として \[\begin{equation}\label{eq:nonlinear} X_{m+1}=\alpha X_m+\beta X_m W_{m+1}+W_{m+1} \end{equation}\] なる非線形なモデルを考えよう.ただし,\(W_1, W_2,\ldots\)は独立で\(\mathcal{N}(0,\sigma^2)\)に従う.この場合,マルコフカーネルは \[ P(x,\cdot)=\mathcal{N}(\alpha x, (1+\beta x)^2\sigma^2) \] で定まる.定義式は自己回帰過程と少し違うだけだが,振る舞いはかなり違う.たとえば\(P(x,\cdot)\)は正規分布だが,\(\beta\neq 0, x\neq 0\)なら\(P^2(x,\cdot)\)はもはや正規分布ではない.
自己回帰過程のように,長期的な振る舞いを検討してみよう.まず,\(X_0=x\)であるとき \[\begin{equation}\label{eq:nonlinear_moment} \mathbb{E}[X_1\mid X_0=x]=\alpha x,\ \mathbb{E}[X_1^2\mid X_0=x]=\alpha^2x^2+(1+\beta x)^2\sigma^2 \end{equation}\] となる.したがって,うまく計算すれば, \[\begin{align*} \mathbb{E}[X_1^2+\delta X_1\mid X_0=x]=\sigma^2 +\gamma(x^2+\delta x) \end{align*}\] となるのがわかるはずだ.ただし,\(\gamma=\alpha^2+\beta^2\sigma^2\)および\(\delta=2\beta\sigma^2/(\gamma-\alpha)\)である.この関係式を再帰的に使えば \[ \begin{align*} \mathbb{E}[X_m^2+\delta X_m\mid X_0=x]&=\sigma^2+\gamma~\mathbb{E}[X_{m-1}^2+\delta X_{m-1}\mid X_0=x]\\ &=\cdots= \sum_{i=0}^{m-1} \gamma^i\sigma^2+\gamma^m~(x^2+\delta x) \end{align*} \] である.だから,\(X_m^2+\delta X_m\)の期待値が発散しないためには\(\gamma=\alpha^2+\beta^2\sigma^2<1\)が必要十分だ.なお,\(X_m^2+\delta X_m\)の期待値が発散しないこととと\(X_m^2\)の期待値が発散しないことは同じことである.自己回帰過程の場合は,\(X_m^2\)の期待値が発散しないための条件は\(\alpha^2<1\)だった.それよりよりやや厳しい条件が必要だ.
7.1.7 p139 定理5.7について (20210308)
「\(x\in, y\in F\)」とあるのは 「\(x\in E, y\in F\)」の誤り.
また,「練習問題4.13から」とあるのは「練習問題4.12から」の誤り.
7.1.8 p140 5.3.3について (20210308)
「第5.1節であつかったギブスサンプリングは\(E=\mathbb{R}\)」 とあるのは 「第5.1節であつかったギブスサンプリングは\(E=(0,1)\)」の誤り.
7.1.9 p144 例5.7 について (20210308)
第12行目で\(p(x^N, y^N\mid \theta)\)とあるのは \(p(x^N\mid y^N,\theta)\)の誤り.
また,下から二行目,正規分布の分散の\(\tau^{-1}\)を掛けるのを忘れている.
7.1.13 p159 6.3.2について (20210308)
上から3行目 \[ \frac{1}{M}\sum_{m=1}^N\|X_m-X_{m-1}\|^2 \] とすべき.
また,Step 2で\(U\le \alpha(X_{n-1}, Y_n)\)とあるのは \(U_n\le \alpha(X_{n-1}, Y_n)\)の誤り.
7.1.14 p160 引き続き6.3.2について (20210308)
下から6,7行目
\[ \sum_{i=1}^n X_{0i}w_{1i},\quad \sum_{i=1}^n X_{0i}\frac{w_{1i}}{\|w_1\|} \] はそれぞれ \[ \sum_{i=1}^d X_{0i}w_{1i},\quad \sum_{i=1}^d X_{0i}\frac{w_{1i}}{\|w_1\|} \] の誤り.
7.1.15 p161 引き続き6.3.2について (20210308)
下から11行目 \[ \sigma^2=\frac{l}{d} \] ではなく \[ \sigma^2=\frac{l^2}{d}. \]
7.1.16 p164 リスト6.3について (20210308)
恥ずかしながら,プログラムにバグが有り,ニュートン・ラフソン法がよく見えているが,実際はもっと悪い.コードを直し,以下のように初期値を十分真値に近く取り直す.
set.seed(1234)
N <- 100
theta <- c(0.3,0.4)
x <- matrix(c(rep(1,N),rnorm(N)), nrow = 2, byrow = TRUE)
p <- exp(as.vector(theta%*% x))/(1+exp(as.vector(theta%*% x)))
u <- runif(N)
y <- as.numeric(u <= p)
f <- function(theta){
sum(as.vector(theta %*% x) * y)-sum(log(1 + exp(as.vector(theta %*% x))))
}
df <- function(theta){
rowSums(t(t(x)*y)) - rowSums(t(t(x) * exp(as.vector(theta %*% x))/(1 + exp(as.vector(theta %*% x)))))
}
ddf <- function(theta){
prob <- exp(as.vector(theta%*% x))/(1+exp(as.vector(theta%*% x)))
-x %*% diag(prob*(1-prob))%*% t(x)
}
data.grid <- expand.grid(s.1 = seq(-5, 8, length.out=200), s.2 = seq(-5, 11, length.out=200))
pv <- numeric(0)
for(i in 1:(dim(data.grid)[1])){
pv <- append(pv,f(as.numeric(data.grid[i,])))
}
M <- 20
theta0 <- c(-1.5,1)
theta <- theta0
theta_mat <- matrix(0, nrow=M, ncol=2)
theta_mat[1,] <- theta0
for(m in 2:M){
theta <- theta - as.vector(solve(ddf(as.vector(theta))) %*% df(theta))
theta_mat[m,] <- theta
}
htheta <-theta
data.fr <- data.frame(x=theta_mat[,1],y=theta_mat[,2], z=1:M)
q.samp <- data.frame(cbind(data.grid, z = pv))
ggplot(q.samp, aes(x=s.1, y=s.2, z=z)) + geom_contour(color=black,alpha=0.5) +
geom_path(data=data.fr,aes(x=x,y=y),lty=2,color=black,alpha=0.5) + geom_point(data=data.fr,aes(x=x,y=y),color=black,alpha=0.5,size=I(2.0))+xlim(-5, 8) + ylim(-5, 11) + xlab(TeX("$\\theta_1$")) + ylab(TeX("$\\theta_2$")) + theme_bw()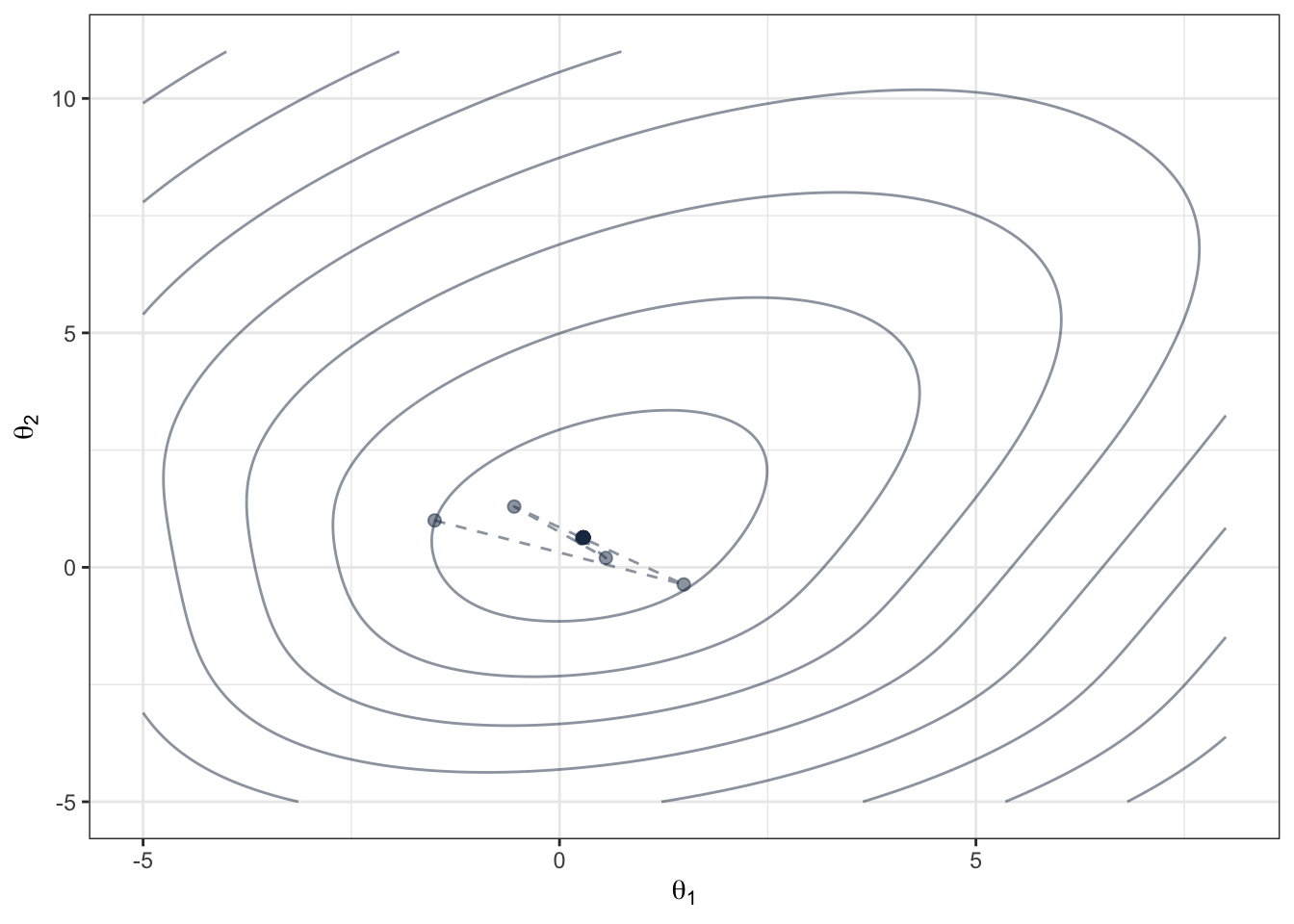
7.2 エラータム 第二刷
7.2.6 p100 定理4.2のあとの解説 (20211125)
「さらに\(|\alpha|>1\)となると,\(x\neq \mu\)なら平均も発散する」とあるが,\(x\)ではなく\(x_0\)とすべき.
7.3 エラータム第三刷
第三刷の修正に関し,岩重文也氏,橋本真太郎准教授(広島大学),千葉航平助教(大阪大学),森田潤一氏(京都女子高校講師)に貴重なご意見を頂いた.この場をお借りして感謝いたします.注:所属はご指摘いただいた当時.
7.3.1 p 31 リスト1.5について
13行目の sqrt の適用範囲が誤り.正しくは下記.
data("ToothGrowth")
x <- ToothGrowth$len
y <- ToothGrowth$supp
sd <- sd(x)
n1 <- sum(y=="OJ")
x1 <- x[y=="OJ"]
mu1 <- sum(x1) / (1 + n1)
sd1 <- sd * sqrt(1 + sum(y=="OJ"))
n2 <- sum(y=="VC")
x2 <- x[y=="VC"]
mu2 <- sum(x2) / (1 + n2)
sd2 <- sd * sqrt(1 + sum(y=="VC"))
q <- 1/(1 + sqrt((1 + n1 + n2) / ((1 + n1) * (1 + n2))) * exp(-(sum(x^2)/(1+n1+n2) - sum(x1^2)/(1+n1)-sum(x2^2)/(1+n2))/(2*sd^2))) # Model Posterior probability of Model mu1=mu0
log10(q/(1-q)) # BayesFactor7.3.2 p 35 リスト1.6について
説明変数の中心化が抜けている.対応する図も少し変わる.
data("airquality")
airquality
x <- airquality$Solar.R[is.na(airquality$Solar.R)+is.na(airquality$Ozone)==0]
x <- x - mean(x) #<<
y <- airquality$Ozone[is.na(airquality$Solar.R)+is.na(airquality$Ozone)==0]
sd <- 31.33
ggplot(airquality,aes(x = Ozone)) +
stat_function(fun=dnorm, args = list(mean = sum(y)/(1+length(y)), sd = sd/sqrt(1+length(y))),color = "blue")+theme_bw()+xlim(35,50)
ggplot(airquality,aes(x = Ozone)) +
stat_function(fun=dnorm, args = list(mean = sum(x*y)/(1+sum(x^2)), sd = sd/sqrt(1+sum(x^2))),color = "blue")+theme_bw()+xlim(0,0.28)
log10(exp(1/(2*sd^2)*sum(x*y)^2/(1+sum(x^2)))*1/sqrt(1+sum(x^2)))#Bayes Factor7.3.3 p 41 線形合同法について
「擬似乱数法RANDUは \(a=65539, b=0, n=2^{31}-1\)とした線形合同法」とあるのは, 「擬似乱数法RANDUは \(a=65539, b=0, \color{red}{n=2^{31}}\)とした線形合同法」の誤り.
7.3.4 p62 2.2.3 近似累積分布関数による乱数生成
rnormの出力が,runifの出力をqnorm関数で変換した逆関数法にように記述しているが,正確には異なる.
実際のrnormのコードによると
#define BIG 134217728 /* 2^27 */
/* unif_rand() alone is not of high enough precision */
u1 = unif_rand();
u1 = (int)(BIG*u1) + unif_rand();
return qnorm5(u1/BIG, 0.0, 1.0, 1, 0);と書かれており,内部で二つの擬似一様乱数を生成して精度を担保している.二つの疑似乱数のうち最初の項が主要項なので,奇数番目に生成した乱数に逆変換法を用いた値はrnormにほとんど一致するが,細かいところでは異なる.以下のように,細かく見ると差を確認できる.
## [1] -0.6264538107 0.1836433242 -0.8356286124## [1] -0.6264538071 0.1836433242 -0.83562862137.3.5 p75 例2.7 ガンマ乱数の生成
ガンマ分布\(\mathcal{G}(\nu, 1)\)からの乱数の生成において,\(\nu >0\)の場合の乱数生成を\(\mathcal{G}([\nu],1)\)からの乱数による棄却法で生成できるように書いているが誤り.
\(\nu<1\)の場合はこの方法は使えない.
7.3.7 p84 定理3.6の証明
\(Y_M/Z_M\)とすべきところが\(Z_M/Y_M\)となっていた. \[ I_M=I~\frac{Y_M}{Z_M}\approx I~\left(1-(Z_M-1)+(Y_M-1)\right) \] とすべき.合わせて次の式も \[ M^{1/2}(I_M-I)\approx I~\left( -M^{1/2}(Z_M-1)+M^{1/2}(Y_M-1)\right)=M^{\color{red}{-}1/2} I\sum_{m=1}^M(-\overline{g}(X_m)+\overline{f}(X_m)) \] とする.\(M\)の指数も誤り.次の式も以下のようになる. \[\begin{align*} \sigma^2&=I^2\operatorname{Var}(-\overline{g}(X_1)+\overline{f}(X_1))\\ &=I^2\left\{\operatorname{Var}(\overline{f}(X_1))-2 \operatorname{Cov}(\overline{f}(X_1),\overline{g}(X_1)) +\operatorname{Var}(\overline{g}(X_1))\right\} \end{align*}\]
7.3.10 p145 例5.7
\(y_n\sim\chi^2_\nu\)の部分等で誤りがあった.第六行目は \[ p(y_n\mid x_n,\theta)\propto p(x_n,y_n\mid\theta)\propto y_n^{1/2}\exp\left(-\left\{\frac{(x_n-\mu)^2}{2\nu} \tau\right\}y_n\right) \color{red}{y_n^{\nu/2-1}\exp\left(-\frac{y_n}{2}\right)} \] とし,次の式とStep 1のガンマ分布は \[ \mathcal{G}\left(\frac{1+\nu}{2}, \frac{(x_n-\mu)^2}{2\nu} \tau+\frac{1}{2}\right) \] とすべき.またStep 2は\(\tau\)が抜けている.
\(\mu\sim \mathcal{N}\left(\frac{\left(\nu^{-1} \sum_{n=1}^Nx_n y_n\right)}{1+\nu^{-1}\sum_{n=1}^N y_n},\left(1+\nu^{-1}\sum_{n=1}^N y_n\right)^{-1}~\color{red}{\tau^{-1}}\right)\)